
George Ziff discovered the “name yourself” law while refining his foreign language teaching methods. The process of learning a foreign language involves expanding one's vocabulary. To speak a language, one must learn the words of that language.
Obviously, picking up a dictionary, reading it cover to cover, and memorizing thousands of words isn't the best approach. After all, some words are more common in the language than others. Some are even rarer. Do you know what a photomontage is? And how is it different from a tintamara?
Therefore, to confidently master a foreign language, you should first learn the most commonly used words, of which there are actually not that many—about 2,000. And it's advisable to learn these words not sequentially, not in alphabetical order.
First, you should master the most frequently used words in the language, then words that are used less frequently, and finally, words used very rarely, for embellishment and individualization of speech. Therefore, if you are going to learn foreign words from a dictionary, it should be a frequency dictionary, not an alphabetical one.
In a frequency dictionary, words are arranged not alphabetically, but by their frequency of occurrence in foreign-language texts. For example, a word that appears 100,000 times in a corpus of one million words will appear before a word with a frequency of 10,000 times per million in the frequency dictionary. This second word, in turn, will appear closer to the beginning of the frequency dictionary than a word that appears only 1,000 times per million words.

Of course, the first words in a frequency dictionary will be function words: prepositions, articles, and others. These words are typically short and carry little semantic load. But within the first ten words, meaningful words will also appear. These are the words that should be given to students first during training. It is at this point that the student, and even more so the teacher, needs a frequency dictionary of the language being studied.
The only thing left to do is calculate the frequency of all words in a given language and rank them in descending order. At least two problems arise here.
First , select a text or group of texts that can represent the entire language. This set is also called a language corpus. A language corpus must be at least 1 million words long and be compiled from a wide variety of sources, from newspaper articles to classical texts. The composition of the language corpus determines the outcome of the entire work. Therefore, selecting the texts that form the language corpus is a responsible undertaking. Moreover, it requires genuine philological insight.
The second problem is actually calculating word frequencies in a given language corpus. Previously, this was simply technically challenging. Now, even a smart schoolchild can write a simple computer program to calculate word frequencies. But this hasn't reduced the number of problems; they've simply reached a new level of complexity.
Perhaps this is why frequency dictionaries appeared relatively recently. The first such English dictionary, “Teacher's Word Book,” was published in 1921. This dictionary included 10,000 of the most common English words. In 1944, it was reissued in an expanded version (30,000 words).
The first frequency dictionary of the Russian language was also published in the United States in 1953. This dictionary contained approximately 5,000 different words. The first frequency dictionary of modern Russian was published in Tallinn in 1963. It included 2,500 of the most common words. In 1977, the first frequency dictionary of the Russian language was published, computer-generated using a text corpus containing 1 million words.
In any case, it's understandable why, as a foreign language instructor at Harvard University, Ziff became interested in the problem of word frequency in language. His first paper in this area was published in 1932.
Zipf and his students of Chinese descent studied word frequencies in languages as distant as Latin and Chinese. This work, and several subsequent studies of word frequencies in natural languages, revealed a pattern later dubbed “Zipf's Law”:
The product of the frequency of occurrence of a word and its position in the frequency dictionary is an approximately constant value .
The meaning of this constant varies across languages.
Zipf's law can also be formulated as follows:
The frequency of occurrence of a word in a text is approximately inversely proportional to its ordinal number in the frequency list .
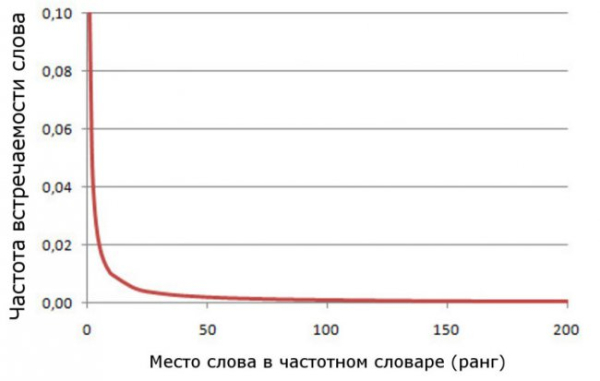
This means that the second-most frequently used word will appear in the corpus approximately half as often as the first. Similarly, the third-most frequently used word will appear three times less often than the first, and so on. The curve describing Zipf's law is a hyperbola, falling off quite rapidly and then trailing off with a nearly horizontal “tail.” The descending portion of this curve contains the most frequently used words, while the tail contains the rarely used words. It is precisely in this portion of the curve that many miracles occur, which will be discussed below.
Zipf's law played a significant role in linguistics because it was the first mathematical regularity discovered in language research. The specific form of the relationship wasn't so important. The main thing was the discovery of a parameter that, when studied, could provide information about the internal structure of language, so to speak. This parameter turned out to be the frequency of words in a text.
For mathematicians and mathematical statisticians, the law discovered by the linguist Zipf was no revelation. From the standpoint of mathematical statistics, Zipf's law is a special case of another statistical distribution, the Pareto distribution. Mark Blau, personal archive
This distribution is named after the famous Italian engineer, economist, and sociologist Vilfredo Pareto (1848–1923) . Pareto's law applies not to abstract objects, but to phenomena we encounter at every step.
The most well-known formulation of this law is called “20 to 80.” For example, 20% of the population in any country owns 80% of the national wealth.
Another manifestation of the Pareto principle is a comfort to the lazy and a delight to perfectionists. Completing 80% of any task requires 20% of the effort. And 80% of the effort is spent on completing the remaining 20%.
pinterest.com
The brilliant mathematician Benoit Mandelbrot (1924–2010) explained Zipf's law from the perspective of information transmission theory. Briefly, Mandelbrot's explanation is as follows.
Language is a means of communication, and its functioning is governed by the same principles that apply to any communication channel. On the one hand, increasing the number of words used to transmit information extends communication time. On the other hand, it reduces the likelihood of error in transmitting a message, thereby reducing communication time by eliminating the need for retransmission.
The compromise between these two conflicting demands leads to shorter words being used more frequently. Mandelbrot's mathematical model of the communication process resulted in a slightly modified version of Zipf's law.
At the same time, the physical meaning of the parameters included in this equation became clear. It even became possible to estimate the speaker's vocabulary, that is, their intelligence.
To be continued …





